Homework Assignment 9
Intermediate Microeconomics (Econ 100A)
Kristian López Vargas
UCSC
Instructions:
You will scan your homework into a single PDF file to be upload.
Only legible assignments will be graded.
Late assignments will not be accepted.
Only two randomly-chosen questions will be graded.
Question 1:
Suppose two firms, Genera Pharma and Futura Pharma, are the only two producers of a specific drug. Genera and Futura have the same formula and sell the drug for the same price, but they are considering whether or not to spend money on an advertising campaign. Each firm can either buy the advertising campaign or not buy it and the following table shows profits for four different scenarios.
| Futura | |||
|---|---|---|---|
| AD | No AD | ||
| Genera | AD | (4,4) | (12,0) |
| No AD | (0,12) | (8,8) | |
-
What is the scenario that maximizes the sum of profits of the two companies?
-
Is there a dominant strategy for each firm?
-
What is the pure strategy Nash Equilibrium?
-
Denote the probability of choosing $AD$ for Futura as $f$ and for Genera as $g$. Find the best response function for Futura, $b_f(g)$, and Genera, $b_g(f)$.
Question 2:
Below table shows the probability of winning for Roger Federer and Rafael Nadal for each of two groundstrokes in tennis: down the line (DL) and crosscourt (CC) $($Taken from UCSB lecture $)$.
| Rafael Nadal | |||
|---|---|---|---|
| DL | CC | ||
| Roger Federer | DL | (5,5) | (8,2) |
| CC | (9,1) | (2,8) | |
- Find the pure strategy NE if any.
- Find the mixed strategy NE if any.
- Find the probability of winning of Federer and Nadal, respectively.
Question 3: Coordination Game
Consider the South Korea - North Korea arms race in which each country could build nuclear missiles or refrain from building them. The payoffs are shown in table below.
| North Korea | |||
|---|---|---|---|
| Build | Refrain | ||
| South Korea | Build | (6,6) | (5,1) |
| Refrain | (3,8) | (12,12) | |
- What are the dominant strategies for each country if any?
- What are the pure strategy NE?
- Denote $n$ as the probability NK will build nuclear missles and $s$ as the probability SK will build nuclear missles. Find the best response function for each country, $b_s(n)$ and $b_n(s)$.
- Find the mixed strategy NE in light of the answer in part 3
Question 4: Centipede game
The centipede game, first introduced by Robert Rosenthal in 1981, is an extensive form game in which two players take turns choosing either to take a slightly larger share of an increasing pot, or to pass the pot to the other player. In other words, player 1 chooses between D $($Down$)$ and A $($Across$)$, where D is pocketing the pot and A is passing the pot to the player 2. Similarly, player 2 chooses between $A$ and $D$.
The payoffs are arranged so that if one passes the pot to one's opponent and the opponent takes the pot on the next round, one receives slightly less than if one had taken the pot on this round.
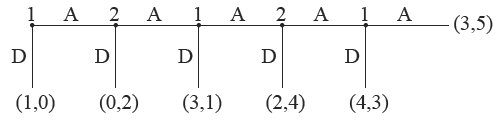
- Find the subgame perfect Nash Equilibrium using backward induction.
Question 5: Ultimatum Game
The ultimatum game is a game in economic experiments. The first player $($the proposer$)$ receives a sum of money and proposes a fair proposal $($F - 5;5$)$ or unfair proposal $($U - 8;2$)$. The second player $($the responder$)$ chooses to either accept $($A$)$ or reject $($R$)$ this proposal. If the second player accepts, the money is split according to the proposal. If the second player rejects, neither player receives any money.

- Find the subgame perfect Nash Equilibrium using backward induction.