Technology

Intermediate Microeconomics (Econ 100A)

Kristian López Vargas

UCSC

Production

  • Production transforms a set of inputs into a set of outputs

  • Inputs / factors of production:
    • labor, land, raw materials, capital
    • Measured in flows
  • Output:
    • The amount of goods and services produces by the firm is the firm’s output.
    • In flow too

Technology

  • What is technology?

    • Knowledge
    • ...determines the quantity of output that is feasible to attain for a given set of inputs.

  • What is a "technological constraint"?

    • Is what separates what is feasible given our current knowledge and what is not.

Technological constraints

  1. Production set: all combinations of inputs and outputs that are technically feasible.

  2. Production function: upper boundary of production set.

    • The production function tells us the maximum possible output that can be attained by the firm for any given (combination) of inputs.
  3. Examples (input, output):
    • (9 hrs of studying per week, final grade of 35) in PS but not efficient (below PF).
    • (9 hrs of studying per week, final grade of 94) not in PS (i.e. not feasible).
    • (9 hrs of studying per week, final grade of 93) in PS and on PF (feasible and efficient).

Production Functions, Sets

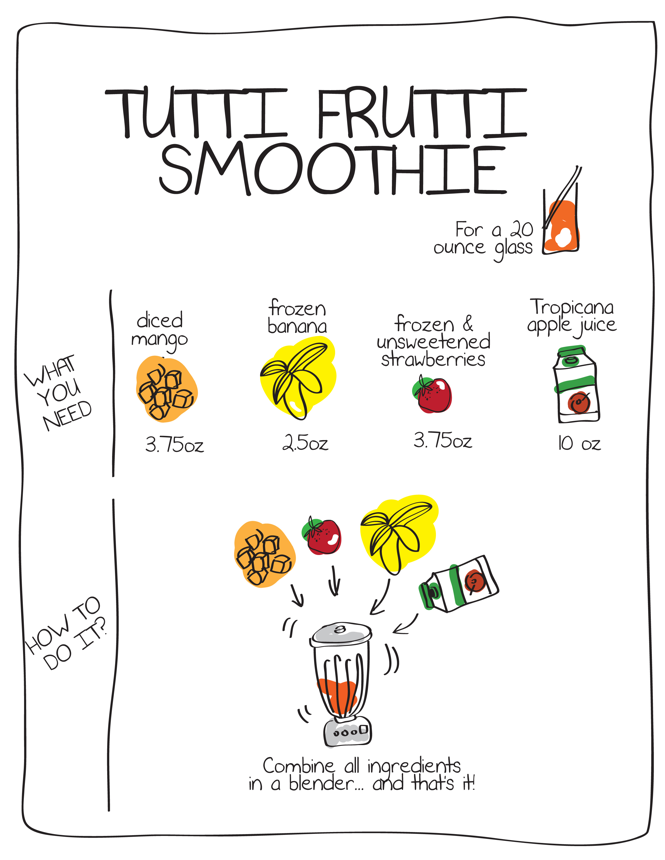
Example - smoothie recipe

Production Functions, Notation, Examples

  • q = f(L, K)
    • q = output (note that book uses $ y $ for output)
    • K = Capital
    • L = Labor
  • Examples:
    • $ q = f(L, K) = L + K $
    • $ q = f(L, K) = L \times K^2 $
    • $ q = f(L) = L^{0.5} $
    • $ q = f(L, K) = min \{ L , K/0.5 \} $
  • Remember: every input and output is expressed in units per unit of time.

Isoquants

  • Isoquants: represent all the combinations of inputs that produce a constant level of output.

  • Isoquants are like indifference curves for preferences, except "isoquants" describe technology not preferences.

  • Isoquants "live" in the space (plane) of factor of production or inputs.

Examples of isoquants

  1. Fixed proportions, complements — one man, one shovel: $ q = \textrm{min} \{ man, shovel\} $

  2. Perfect substitutes — pen, pencils: $ q = pen + pencils $

  3. Cobb Douglass: $ q = A L^a K^b $

  4. Warning: a monotonic transformation of f(K,L) does not give the same technology!

  • Exercise: what type of tech is a cooking recipe?

Assumptions - well-behaved technologies

  1. Monotonic — more inputs produce more output

  2. Convexity — averages produce more than extremes

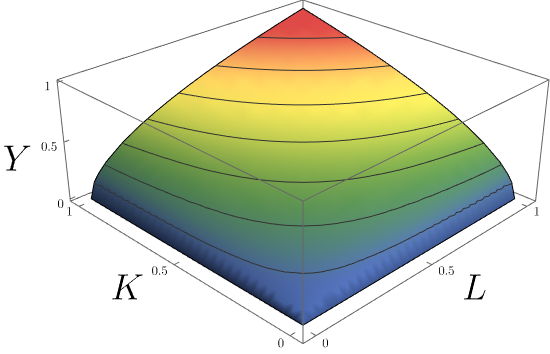
3-D version of a C-D production function

Marginal Product

  • $ MP_L $ is how much extra output you get from increasing the usage of labor holding K constant.

  • $ MP_L = \frac{ ∂f(L,K) }{∂L} $

  • Similarly: $ MP_K = \frac{ ∂f(L,K) }{ ∂K } $

  • Examples:
    • $ q = f(L, K) = L + K $
    • $ q = f(L, K) = L \times K^2 $
    • $ q = f(L) = L^{0.5} $
    • $ q = f(L, K) = min \{ L , K/2 \} $

Average product $ {AP}_L $

  • $ AP_L $ is the per-worker output: $ AP_L = \frac{ f(L,K) }{ L} $

  • $ AP_K $ is the per machine output: $ AP_K = \frac{ f(L,K) }{ K } $

  • Examples:
    • $ q = f(L, K) = L + K $
    • $ q = f(L, K) = L \times K^2 $
    • $ q = f(L) = L^{0.5} $
    • $ q = f(L, K) = min \{ L , K/2 \} $

APL and MPL

  • If $ MP_L > AP_L $ , can it be that $ AP_L $ is decreasing? Nope

  • If $ MP_L < AP_L $ , can it be that $ AP_L $ is increasing? Nope

  • If $ MP_L $ and $ AP_L $ cross, where/how do they cross?

Technical rate of substitution TRS

  • Similar to MRS

  • Technical rate of substitution (TRS): Suppose you increase $ L $ by $ \Delta L $. How much can you reduce K ( $ - \Delta K $ ) such that production level is not altered?

  • Mathematically, TSR is the derivative of K with respect to L, along one isoquant curve: $ TRS = \frac{ dK }{ dL } = - \frac{ MP_L }{ MP_K } $

  • Examples: do Cobb-Douglas and linear production.

Diminishing marginal product / returns

  • Diminishing marginal returns: More of a single input produces more output, but at a decreasing rate:
    • Example: $ q = f(L, K) = L^{0.5} K^2 $

  • Diminishing TRS equivalent to convexity.

  • (!) There is a difference between diminishing returns (MPs) and diminishing TRS (!)

    • Example: $ q = L \times K $

    • $ MP_L $ is not diminishing but $ TRS $ is decreasing.

Isoquants and Returns to Scale

Returns to scale

  • Is this scalable?
    • Often, firms need to grow! Can I just multiply the amount of inputs?
    • That depends largely on the firms’ technology.
  • What happen to my output if I double ALL my inputs?
    • Doubling inputs: $ f(2L, 2K) $ what is the resulting $ q $ ?
    • Similarly $ f(3L, 3K) $ ?
    • Similarly $ f(1.1L, 1.1K) $ ?

Returns to scale - definition

Production function exhibits:

  • Constant returns to scale (CRS): when a percentage increase in inputs is followed by the same percentage increase in output.
    • Example: doubling inputs doubles output: $ f(2L, 2K) = 2f(L, K) $
  • Increasing returns to scale (IRS): when a percentage increase in inputs is followed by a larger percentage increase in output.
    • Example: $ f(2L, 2K) > 2f(L, K) $
  • Decreasing returns to scale (DRS): when a percentage increase in inputs is followed by a smaller percentage increase in output.
    • Example: $ f(2L, 2K) < 2f(L, K) $

Returns to scale - intuition

Some technologies allow for proportional scaling up of your production operation. Some other technologies do not. Why?

  1. CRS: Easy replication (e.g. flyer distribution, data centers. Think of other examples)

  2. IRS: Occurs often with greater specialization of L and K (e.g. a larger plant more productive than two small plants).

  3. DRS: Occurs often because of the difficulty in organizing/coordinating/searching activities as firm size increases (e.g. mining).

Returns to scale - the math

For $ t>1 $, the production function $ f(L,K) $ exhibits CRS/IRS/DRS when:

  1. CRS: $ f(tL,tK) = t f(L,K) $

  2. IRS: $ f(tL,tK) > t f(L,K) $

  3. DRS: $ f(tL,tK) < t f(L,K) $

Returns to scale - examples

  • $ q = f(L, K) = L + K $
  • $ q = f(L, K) = L \times K^2 $
  • $ q = f(L) = L^{0.5} $
  • $ q = f(L, K) = min \{ L , K/2 \} $

Returns to scale - graphics

Returns to scale - local notion

  • "Returns to scale" are a local notion!

  • Some prod functions have "global" returns to scale (e.g. $ q = L K $ ), but not all.

  • Example: $ q = f(L,K) = (L+K) + (K+L)^2 - 0.1 (K+L)^3 $

Long run and short run of the firm

  1. If all factors can be adjusted, the firm is in the "long run"

  2. If at least one factor cannot be adjusted, the firm is in the "short run"

  3. That is, we are in the short run (SR) when some factor(s) must stay fixed.

    • Typically, we hold $ K $ constant at level $ \bar{K} $ in the SR.

    • So the typical production function in the short run is written as:


$$ q = f(L, \bar{K} ) $$

Explore more graphics to understand better

http://www2.hawaii.edu/~fuleky/anatomy/anatomy.html