Demand

Intermediate Microeconomics (Econ 100A)

UCSC - 2020

---

Demand function

• "Optimal bundle" for generic prices and income = Demand Function.

• The "optimal bundle" changes when income or prices change: that is why we call it demand function.

---

Demand function

• For a specific utility (preferences) and given set of income and prices, we have learned how to find the optimal bundle.

• If you solve this, so called, consumer's problem for generic income and prices $ (p_1,p_2,m) $, what you obtain is the demand function: $ x_1^{*}(p_1,p_2,m) $.

• For example, if utility is Cobb-Douglas, then $ x_1^{*} (p_1,p_2,m) = \frac{a m}{ (a+b) p_1} $

A consumer's demand function indicates the optimal choice for a given set of prices and income.

---

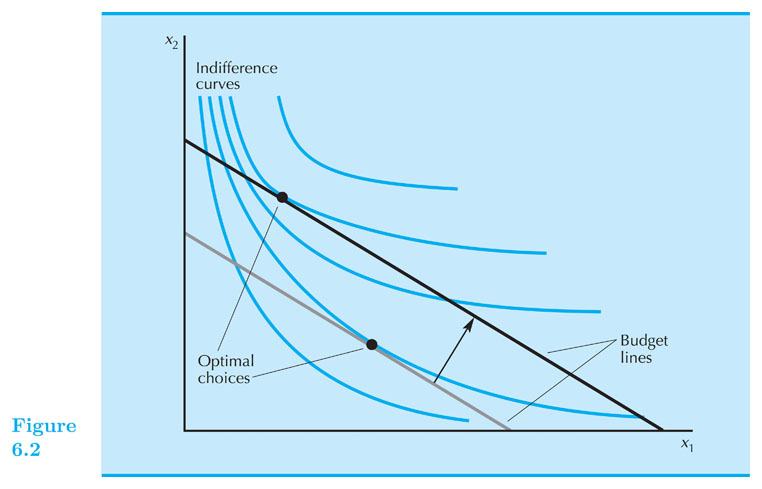
Changes in income

$ x_1 = x_1(p_1,p_2,m) $

• How does the optimal consumption of $ x_1 $ changes with changes in income? $ \frac{\partial x_1}{ \partial m } $ Vs. $ 0 $

• A normal good: its consumption increases when income increases.

  • $ \frac{\partial x_1}{ \partial m } > 0 $
  • Do graph

• An inferior good: its consumption decreases when income increases.

  • $ \frac{\partial x_1}{ \partial m } < 0 $
  • Do graph

---

Engel Curve

• The Engel Curve maps each level of income to the optimal consumption of a good, holding prices constant.

---

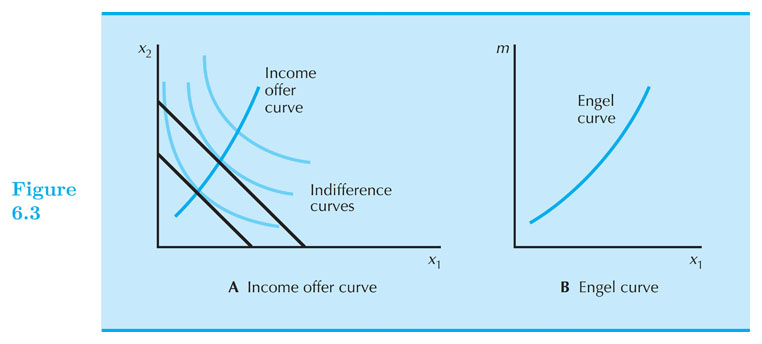
Engel Curve - Inferior good

---

---

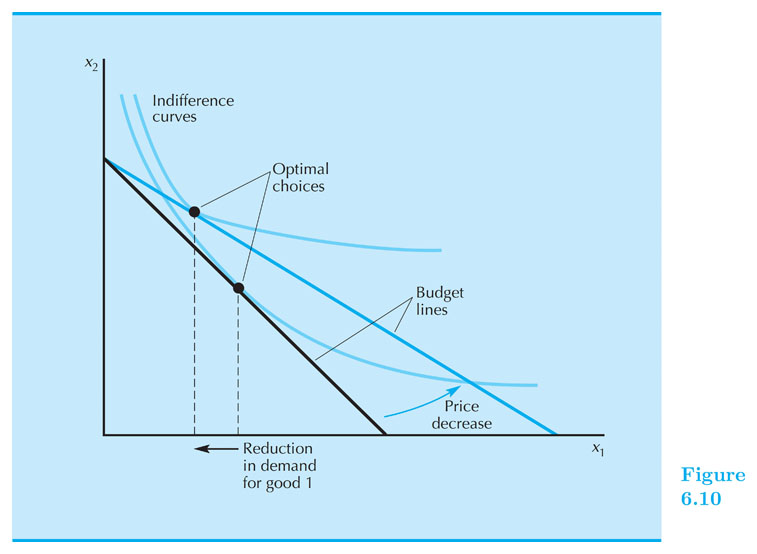
Changes in prices

• $ \Delta p_1 $ tilts or pivots the budget line.

• How does the optimal consumption of $ x_1 $ changes with changes in $ p_1 $? $ \frac{\partial x_1}{ \partial p_1 } $ Vs. $ 0 $

• Ordinary good: its consumption decreases when its price increases.

  • $ \frac{\partial x_1}{\partial p_1} < 0 $
  • Do graph

• Giffen good: its consumption increases when its price increases.

  • $ \frac{\partial x_1}{\partial p_1} > 0 $
  • Do graph

---

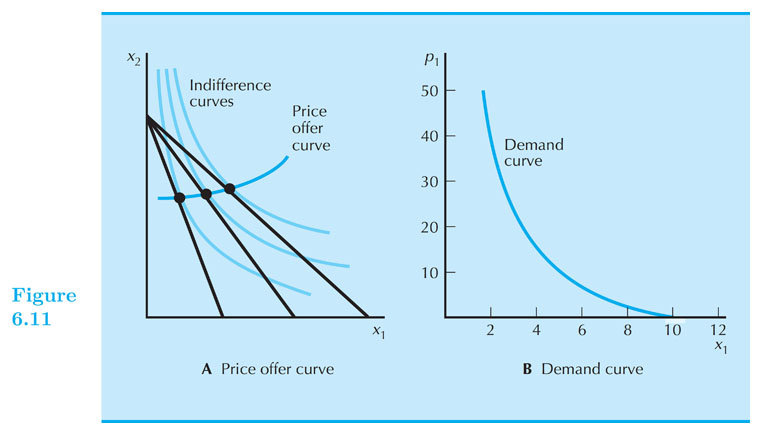
Demand curve

• Demand curve: describes the relationship between the optimal choice of a good and its price, with income and other prices held constant.

---

Giffen Good

---

---

Substitutes and Complements

• Gross Substitutes: $ \frac{\partial x_1}{ \partial p_2 } > 0 $

• Gross Complements: $ \frac{\partial x_1}{ \partial p_2 } < 0 $