Utility

Intermediate Microeconomics (Econ 100A)

Kristian López Vargas

UCSC

One additional assumption on preference relations

• Continuity:

  • A small change in a bundle can only cause small changes to the preference rankings and level.

  • Put differently, if A is preferred to B, then situations suitably close to A must also be preferred to B.

Utility Function

• Main idea: instead of preference relations, we can describe a consumers' preferences using utility functions.

• Intuition: A utility function assigns a "satisfaction level" (a number) to each alternative or bundle.

• Instead of saying: $ iPhone7 \succ Galaxy8 $, we say $ U(iPhone7) > U(Galaxy8) $

• Instead of saying: $ (2 \textrm{ Beers}, 3 \textrm{ Pizzas} ) \succ (1 \textrm{ Beers}, 4 \textrm{ Pizzas} ) $, we say $ U(2, 3) > U(1, 4) $

Utility Function

• But, how does a preference relations and a utility function connect?

• If a consumer's preference relations are:
  1. complete,
  2. transitive,
  3. continuous

• Then, these preferences can be represented by a (continuous) utility function.

• Note on reflexivity, monotonicity, convexity.

Utility Function

• When do we say that we a utility function represents someone's preference relations?

• A utility function $ U(x) $ represents a preference relation $ \succsim $ when:

  • $ x’ \succ x’’ \iff U(x’) > U(x’’), ~~ $ for any $ x' $ and $ x'' $

  • $ x’ \succsim x’’ \iff U(x’) \geq U(x’’) ~~ $, for any $ x' $ and $ x'' $

  • $ x’ \sim x’’ \iff U(x’) = U(x’), ~~ $ for any $ x' $ and $ x'' $

• Intuitively, $ U() $ represents a preference relation if it yields the same ranking of alternatives.

Utility Function

• That is, like preference relations, utility is an ordinal (i.e. ordering) concept.

• If, for example, $ U(x) = 6 $ and $ U(y) = 2 $ then bundle $ x $ is strictly preferred to bundle $ y $. But we cannot say: " $ x $ is preferred three times as much as is $ y $ ".

Utility Functions & Indifference Curves

• An indifference curve contains equally preferred bundles.

• In terms of utility, all bundles in an indifference curve give the same utility level:

  • If $ x \sim y $, $ \iff $ $ U(x) = U(y) $.

• In other words, indifference curves are the level curves of utility functions.

Utility Functions & Indiff. Curves - Example!

$ u(x_1, x_2) = x_1 ~ x_2 $

Utility Functions & Indifference Curves

• A more complete collection of indifference curves describes more fully the consumer’s preferences (aka indifference map).

Utility functions (are not unique)

• The preferences of a certain consumer can be described/represented by more than one utility function.

• That is, there is no unique utility function for a preference relation.

• Two utility functions $ U() $ and $ V() $ represent the same preferences, if we can obtain $ V() $ by applying a strictly increasing function on U():

• That is, if we can write $ V = f( U() ) $ where $ f() $ is strictly increasing.

• [ ask students about strictly increasing functions ]

Utility functions (are not unique) - Example 1!

• Suppose $ U(x_1,x_2) = x_1 x_2 $ represents some preferences.

• You have bundles $ (4,1), (2,3) $ and $ (2,2) $.

• Under this utility function: $ U(2,3) = 6 > U(4,1) = U(2,2) = 4 $;

• Therefore, we know that: $ (2,3) \succ (4,1) \sim (2,2) $.

Utility functions (are not unique) - Example 1!

• Suppose we define $ V = U^2 $.

• Then, $ V(x_1,x_2) = (x_1 x_2)^2 = x_1^2 x_2^2 \quad $

• ...and so, $ V(2,3) = 36 > V(4,1) = V(2,2) = 16 $

• SO! again $ (2,3) \succ (4,1) \sim (2,2) $.

• That is, $ V() $ preserves the same order as $ U() $ and therefore represents the same preferences.

Utility functions (are not unique) - Example 2!

• Suppose we define $ W = 2U + 10 $.

• Then, $ W(x_1,x_2) = 2 (x_1 x_2) + 10 $

• ...and so, $ W(2,3) = 22 > W(4,1) = W(2,2) = 18 $

• SO! again! $ (2,3) \succ (4,1) \sim (2,2) $.

• That is, $ W() $ preserves the same order as $ U() $ and therefore represents the same preferences.

Goods, Bads and Neutrals

• A good is a commodity unit which increases utility (gives a more preferred bundle).

• A bad is a commodity unit which decreases utility (gives a less preferred bundle).

• A neutral is a commodity unit which does not change utility (gives an equally preferred bundle).

• For home: Draw indifference curves for each of them

Drawing an Indifference Curve

1. Identify the utility function: $ U(x_1, x_2) $.

2. Set the utility level to a constant level $ k $: $ U(x_1, x_2) = k $.

3. Solve for $ x_2 $ in the previous equation to obtain a generic indifference curve.

4. Give $ k $ an arbitrary value and draw the curve.

5. To draw another curve, set $ k $ equal to another value and draw again.

Drawing an Indifference Curve - Example!

1. Utility: $ U(x_1, x_2) = x_1^{0.5} x_2 $

2. Utility at a constant level: $ x_1^{0.5} x_2 = k $

3. Solve for x₂: $ x_2 = \frac{k}{x_1^{0.5}} $.

4. Give $ k $ a value: $ x_2 = \frac{ 10 }{x_1^{0.5}} $. Draw!

5. Give $ k $ another value: $ x_2 = \frac{ 20 }{x_1^{0.5}} $. Draw!

• Try with other functions... for example: $ U(x_1, x_2) = x_1 + x_2^{0.5} $

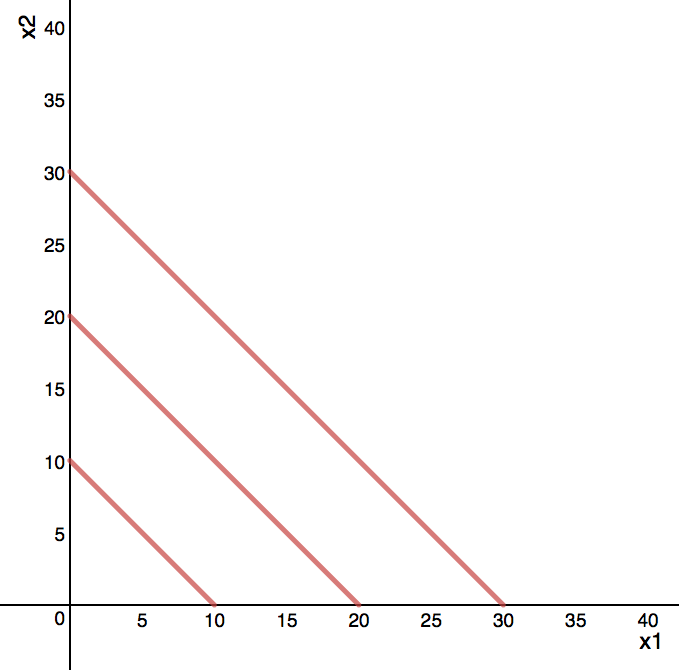
Typical utility fns: perfect substitutes

• General: $ ~ U(x_1,x_2) = \alpha x_1 + \beta x_2 ~~ $, for $ \alpha, \beta > 0 $

• Example: $ ~ U(x_1,x_2) = x_1 + x_2 $

Typical utility fns: perfect substitutes

Typical utility fns: perfect complements

• General: $ ~ U(x_1,x_2) = \textrm{min} \{ \frac{x_1}{\alpha}, \frac{x_2}{\beta} \} ~~ $, for $ \alpha, \beta > 0 $.

• Example: $ ~ U = \textrm{min} \{ x_1, x_2 \} ~~ $

Typical utility fns: perfect complements

Typical utility fns: Cobb-Douglas

General $ U(x_1,x_2) = x_1^a x_2^b $ with a > 0 and b > 0

Examples:

• $ U(x_1,x_2) = x_1^{0.5} x_2^{0.5} \quad $ (that is, $ a = b = 1/2 $)

• $ U(x_1,x_2) = x_1 x_2^3 \quad $ (that is, $ a = 1, b = 3 $)

• $ U(x_1,x_2) = x_1^{2} x_2^{0.75} \quad $ (that is, $ a = 2, b = 0.75 $)

Typical utility fns: Cobb-Douglas

Marginal Utility

• Marginal means “incremental”.

• The marginal utility of commodity $ x_1 $ is the rate-of-change of total utility as the quantity of commodity $ x_1 $ consumed increases.

• $ MU_{x_1} = \frac{\partial U}{\partial x_1} $ and $ MU_{x_2} = \frac{\partial U}{\partial x_2} $

• To know whether $ MU_{x_1} $ is increasing or decreasing in $ x_1 $, we take the derivative of $ MU_{x_1} $ with respect to $ x_1 $. That is, we calculate: $ \frac{\partial MU_{x_1}}{\partial x_1} $

Marginal Utilities - Cobb-Douglas Example!

Utility: $ U(x_1,x_2) = x_1^{0.5} x_2^2 $

Marginal Utilities:

$ MU_{x_1} = \frac{\partial U}{\partial x_1} = 0.5 x_1^{-0.5} x_2^2 $

$ MU_{x_2} = \frac{\partial U}{\partial x_2} = 2 x_1^{0.5} x_2^1 $

Marginal Utilities - Perf. Substitutes Example!

Utility: $ U(x_1,x_2) = a x_1 + b x_2 $

Marginal Utilities:

$ MU_{x_1} = \frac{\partial U}{\partial x_1} = a $

$ MU_{x_2} = \frac{\partial U}{\partial x_2} = b $

Marginal Utilities - Perf. Complements Example!

• Utility: $ U(x_1,x_2) = min \{ x_1 , x_2 \} $

  • Not differentiable at the kinks.

Marginal Utilities and the MRS

Claim: $ MRS \equiv \frac{d x_2}{d x_1} = - \frac{ MU_{x_1} }{ MU_{x_2} } $

Here is the math:

0. Remember, the equation for an indifference curve is: $ U(x_1,x_2) = k $, where satisfaction, $ k $, is a constant.

1. Do total differentiation: $ \frac{\partial U}{\partial x_1} d x_1 +
   \frac{\partial U}{\partial x_2} d x_2 = d k $,

2. But $ dk = 0 $ since $ k $ is a constant, and $ \frac{\partial U}{\partial x_i} $ can be replaced by $ MU_{x_i} $. That is: $ MU_{x_1} d x_1 + MU_{x_2} d x_2 = 0 $

3. We solve for $ \frac{d x_2}{d x_1} $ and we get: $ \frac{d x_2}{d x_1} = - \frac{ MU_{x_1} }{ MU_{x_2} } $

Marginal Utilities and the MRS - Examples:

• If $ U = x_1^{2} x_2 $,
• Then: $ MRS = - \frac{MU_{x_1}}{MU_{x_2}} = $ $ - \frac{2 x_1 x_2}{ x_1^2 } = $ $ - 2 \frac{ x_2 }{ x_1 } $

• If $ U = x_1 x_2^{0.5} $,
• Then: $ MRS = - \frac{MU_{x_1}}{MU_{x_2}} = $ $ - \frac{x_2^{0.5}}{ x_1 0.5 x_2^{-0.5}} = $ $ - 2 \frac{ x_2 }{ x_1 } $

• If $ U = x_1 + 5 x_2 $,
• Then: $ MRS = - 1/5 $