Rationality in Economics - Behavioral Postulates
A decision maker knows what he/she likes/enjoys and chooses his/her most preferred alternative among the available ones.
To say something about his/her behavior, we must model decision makers’ preferences.
Basics of Preferences Relations
John: apple better than Mango, apple better than banana, mango better than banana.
![]()
Basics of Preferences Relations
Alí, Bob, Carlos, … , John, … ,Wei
![]()
…
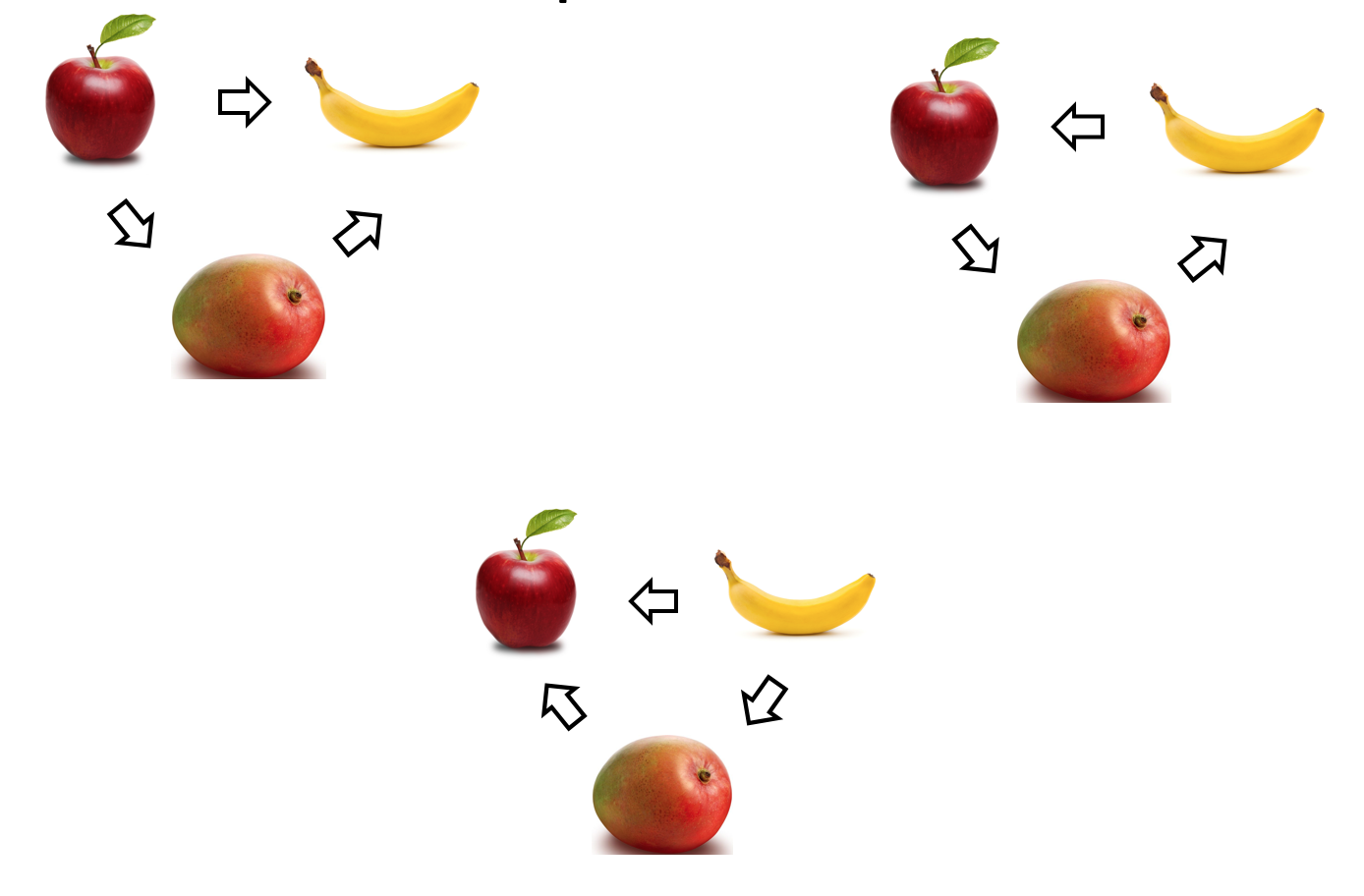
Basics of Preferences Relations
![]()
Preference Relations
Comparing two different consumption bundles, $ x $ and $ y $ in the consumption space:
Strict preference “$ x \succ y $” : x is strictly more preferred than is y
Weak preference “$ x \succsim y $” : x is as at least as preferred as is y
Indifference “$ x \sim y $” : x is equally preferred as is y
Assumptions on Preference Relations
Assumptions on Preference Relations (1): Completeness
Assumptions on Preference Relations (2): Transitivity
- Transitivity:
- If x is at least as preferred as y, and
- y is at least as preferred as z, then:
- x is at least as preferred as z.
- That is, if $ x \succsim y $ and $ y \succsim z $ implies $ x \succsim z $
Assumption on Preferences (3): More is better (monotoniticy)
More is Better / Monotonicity: * All else the same, more of a “good” commodity is better than less. * $ (5.01, 20) \succ (5, 20) $
Assumption on Preferences (3): More is better (monotoniticy)
- This assumption implies that indifference sets are:
- Curves! (not thick bands)
- Downward sloped! (think about it)
![]()
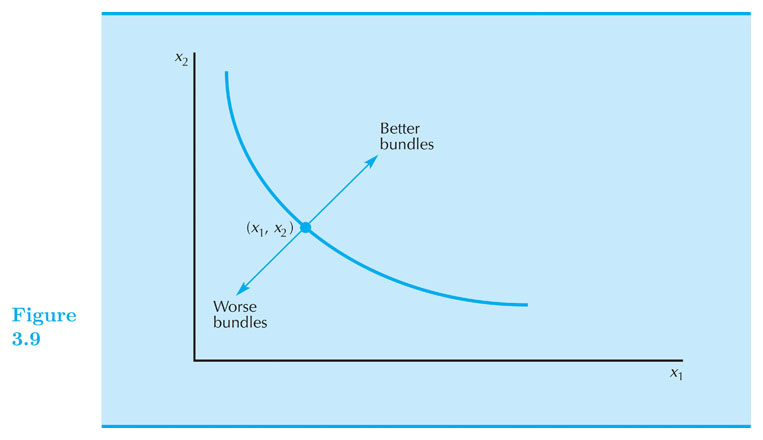
Preferences in the Commodity Space
- Recap: the Commodity Space is the positive quadrant of the n-dimensional plane ($ \Re_{+}^n $) where these baskets or bundles live.
![]()
Indifference Curves or Indifference Sets
Indifference Curves or Indifference Sets (of consumer i):
A set of bundles that a consumer regards as equal.
Take bundle $ x $. The set of all bundles equally preferred to $ x $ makes the “indifference curve” containing $ x $. We denote this set by $ I(x) $.
All the bundles $ y $ in this set have this property: $ y \sim x $.
Since an indifference “curve” is not necessarily a “curve”, we might want to call it indifference “set”.
Indifference Curve (example)
- E.g.: $ (3, 4) \sim (1, 12) $
Weakly preferred set WP(x)
- WP(3,4) is the shaded area
Is there only one indifference curve?
No! Typically, there are infinite.
In most cases it makes sense we talk and draw several (“the indifference map”).
Goods Vs. Bads Vs. Neutrals
Assume $ x_2 $ is a good: more is better.
Draw and IC for each case:
$ x_1 $ is a good.
$ x_1 $ is a bad.
$ x_1 $ is a neutral.
Home exercise:
- Can two distinct indifference curves cross each other?
Assumption on Preferences (4): Convexity
(Weak) Convexity:
Mixtures of bundles are (weakly) preferred to the bundles themselves.
Example: If the 50-50 mixture of the bundles $ x $ and $ y $ is formed like this $ z = (0.5) x + (0.5)y $. Then $ z $ is at least as preferred as $ x $ OR $ y $.
Assumption on Preferences (4): Convexity
![]()
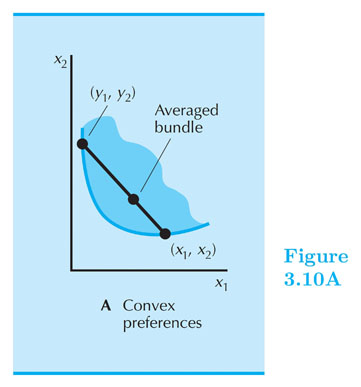
Assumption on Preferences (4): Convexity
- Example of preferences that do not satisfy convexity
![]()
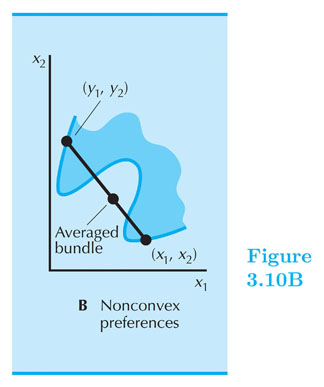
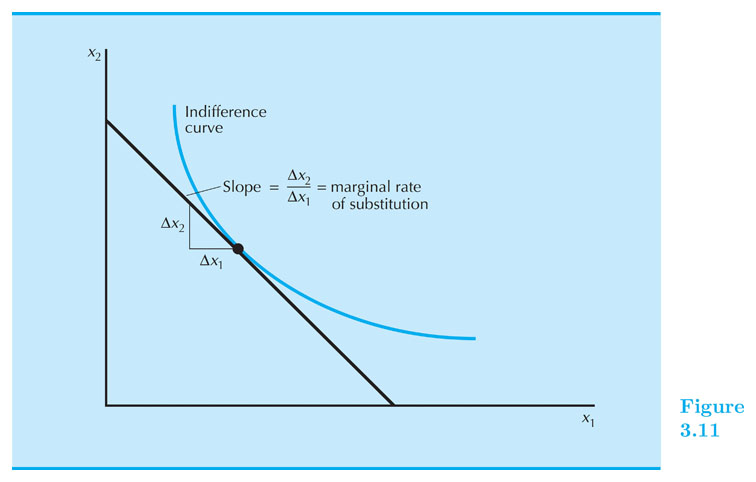
Slope of an Indifference Curve
The slope of an indifference curve is its marginal rate-of-substitution or MRS.
MRS is the rate at which the consumer is only just willing to exchange/substitute commodity 2 for a small amount of commodity 1.
$ MRS = \frac{d x_2} {d x_1} $ along one indifference curve.
Types of Preferences: Perfect Substitutes
Types of Preferences: Perfect Complements
If a consumer always consumes commodities 1 and 2 in fixed proportion (e.g. one-to-one), then the commodities are perfect complements to the consumer.
Only the number of pairs in the fixed proportion matter to the consumer. Examples?
