Budget Constraint
Intermediate Microeconomics (Econ 100A)
UCSC
Consumption Choice Sets
A consumption choice set is the collection of all consumption alternatives available to the consumer.
What does constrain actual consumption?
- Budget, time and other resource that are limited.
Consumption bundle
A consumption bundle containing $ x_1 $ units of good 1, $ x_2 $ units of good 2 and so on up to $ x_n $ units of good $ n $ is denoted by the vector $ ( x_1, x_2, … , x_n ) $.
Prices of goods are denoted by $ p_1, p_2, … , p_n $, respectively.
We often use just $ p $ to denote the vector of prices.
Affordable Bundles - Budget Constraints
Suppose prices are $ p_1, p_2, … , p_n $ and a consumer has $ m $ as income.
We assume all prices and income are strictly positive.
- Question:
- When is a consumption bundle $ (x_1, … , x_n) $ affordable at those given prices and with the given income?
Affordable Bundles - Budget Constraints
Answer:
when $ p_1 x_1 + … + p_n x_n \leq m $
That is, the bundle is affordable when the consumer purchases it and does not exhaust her income.
“Budget line” or “budget constraint”
The set of bundles that are just affordable in that they exhaust the consumer’s income, conform the consumer’s budget constraint or budget line.
Formally, we represent this set as:
$ BL(p,m) = \{ ( x_1 ,…, x_n ) :p_1 x_1 + … + p_n x_n = m \} $
- For simplicity, we will only work with consumption quantities $ x_1, … , x_n $ that equal or greater than zero.
Budget Set
- The consumer’s budget set is the set of all affordable bundles;
$ B(p_1, … , p_n, m) = \{ (x_1, … , x_n) :p_1 x_1 + … + p_n x_n \leq m \} $
- Notice that the budget constraint (or budget line) is the upper boundary of the budget set.
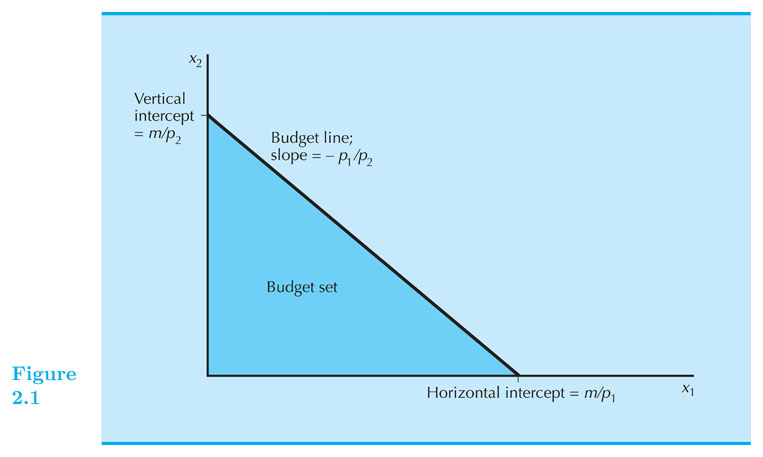
Budget for Two Commodities
- $ p_1 x_1 + p_2 x_2 = m $. Affordable set, intercepts, slope.
Finding the slope of the BC
Budget line: $ p_1 x_1 + p_2 x_2 = m $
Solve for $ x_2 $ :
$ p_2 x_2 = m - p_1 x_1 $
$ x_2 = \frac{m}{p_2} - \frac{p_1}{p_2} x_1 $
Therefore the slope is: $ - \frac{p_1}{p_2} $
What is the interpretation of the slope? It is the relative price.
Budget for Three Commodities
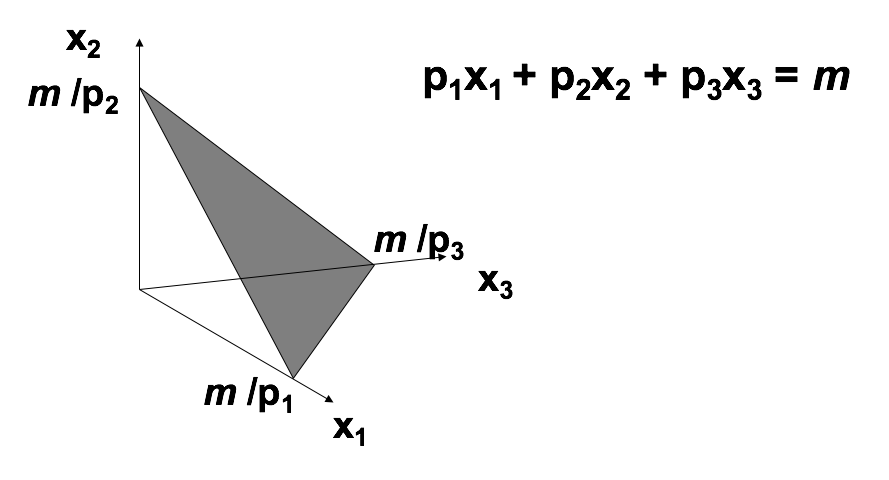
Example of BC
Good one is beer (good 1) and orange juice (good 2).
Suppose $ p_1 = 3 $ and $ p_2 = 1 $.
Income = 100
slope = - 3: Consumer need to give up (buy less) 3 oz. of orange juice to afford (be able to buy) 1 additional oz of beer.
You can use the market to transform three units of OJ into one unit of beer, at the current prices. Therefore the term of relative price.
Changes in the BC
The budget constraint and budget set depend upon prices and income. What happens as prices or income change?
Income change?
Prices change?
Makler’s EconGraphs
Introducing EconGraphs
Income Increases
Increases in income m shift the constraint outward in a parallel manner, thereby enlarging the budget set and making more bundles affordable.
Decreases in income m shift the constraint inward in a parallel manner, thereby shrinking the budget set and making fewer bundles affordable.
Which one is good for the consumer?
Income Changes
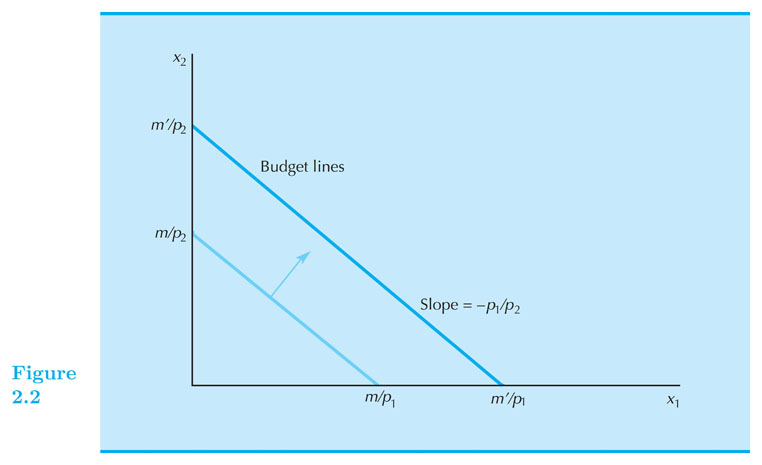
- What bundles become unaffordable or newly affordable?
$ p_1 $ increases
If $ p_1 $ increases from $ p_1 $ to $ p_1’ $:
Budget constraint pivots: slope get steeper from $ -p_1 / p_2 $ to $ -p_1’/p_2 $
Increasing the price of one commodity pivots the constraint inward.
Some old choices are lost, so increasing one price could make the consumer worse off.
Price Changes
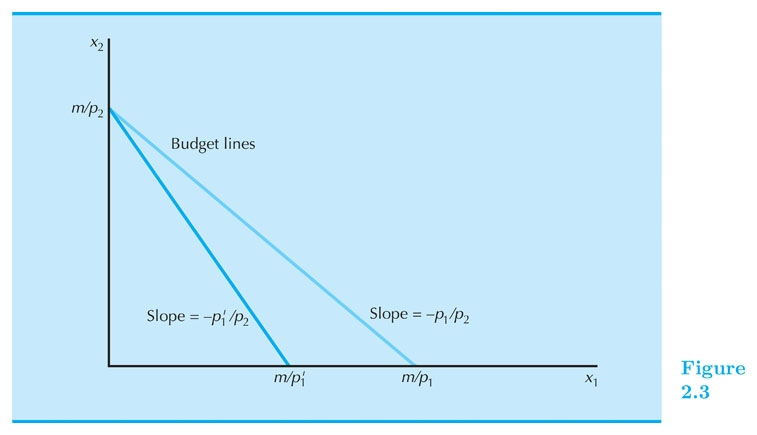
- What bundles become unaffordable or newly affordable?
Ad Valorem Sales Taxes
In ad valorem taxes, we pay an additional percentage of price per-unit in taxes.
An ad valorem sales tax levied at a rate of 5% increases all prices by 5%, from $ p $ to $ 1.05 p $ .
An ad valorem sales tax levied at a rate of t increases all prices by tp from p to (1+t)p.
BC under a uniform sales tax: $ (1+t) p_1 x_1 + (1+t) p_2 x_2 = m $
BC under a sales tax only on good 1 $ (1+t) p_1 x_1 + p_2 x_2 = m $
Do the graph!
Exercise: In kind gifts
Consumer receives $ g_1 $ units of good one as a gift.
Case 1: you can sell (trade) the gift if you want to.
Case 2: you cannot sell the gift.
Draw the budget line.
Exercise: The Food Stamp Program
Coupons that can be exchanged only for food.
How does a food stamp alter a family’s budget constraint?
Suppose $ m = {$}400 $ , $ p_F = {$}1 $ and the price of “other goods” is $ p_G = {$}1 $.
The budget constraint is then $ F + G = 400 $
Draw the budget line.
The Food Stamp Program
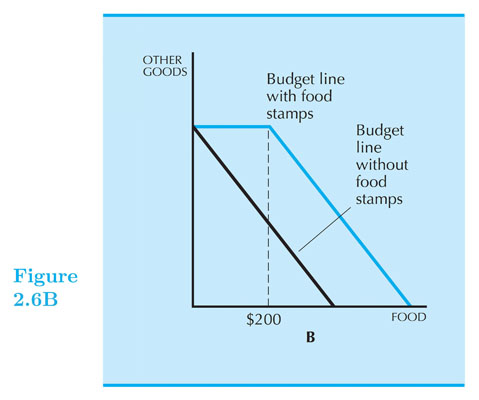
The Food Stamp Program
- What if food stamps can be traded on a black market for $0.50 each?
Other important cases
What if both, prices and income, double?
What if there are bulk discounts for units beyond a threshold?
What if there are quantity penalties for units beyond a threshold?