Cost Curves

Intermediate Microeconomics (Econ 100A)

Kristian López Vargas

UCSC

Cost Curves - Average Costs

• Total cost: $ c(q) = c_v(q) + F $

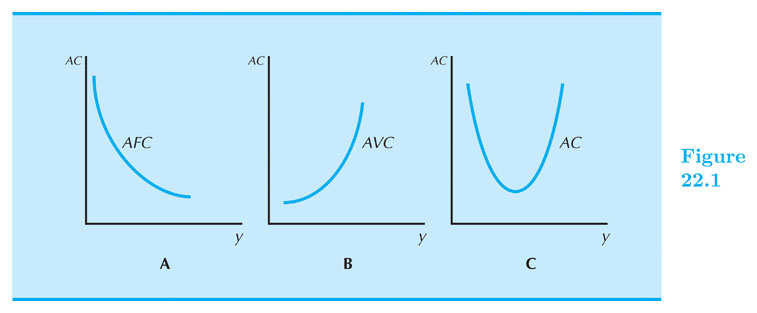
• Average Cost: $ AC(q) = \frac{c(q)}{q} = \frac{c_v(q)}{q} + \frac{F}{q} $

• That is: $ AC(q) = AVC(q) + AFC(q) $

• Notice FC does not depend on $ q $, but AFC does depend on $ q $.

• Can AFC increase in $ q $

Average Costs

Marginal Cost

• Marginal cost is the change in cost due to change in output

• $ c’(q) = \frac{ ∂c(q) }{ ∂q } = \frac{ ∂c_v(q) }{ ∂q } $

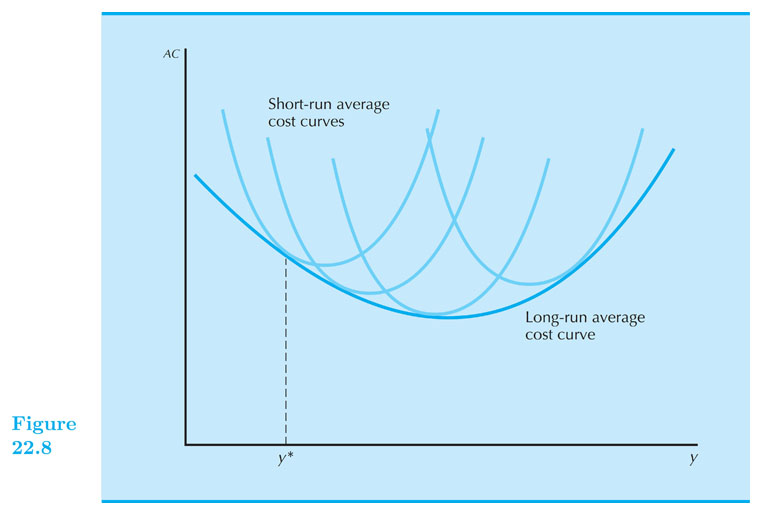
The geometry of total cost, AC, AVC and MC

• MC: is the slope of a tangent line of c(q) at q level.

• AC: is the slope of the ray from the origin to c(q) at q level.

• See document camera side

• https://www.econgraphs.org/graphs/micro/producer_theory/cost_curves

Some relations of Cost Curves

• Marginal cost equals AVC at zero units of output

  • Because AVC starts at the origin.

• MC: crosses at minimum points of AC and AVC.

  • MC < AC when AC is decreasing and MC > AC when AC is increasing.

Cost Curves

Cost Curves - Example:

• $ c(q) = 1 + q^2 $

• $ c_v(q) = ? $

• $ FC(q) = ? $

• $ AVC(q) = ? $

• $ AFC(q) = ? $

• $ AC(q) = ? $

• $ MC(q) = ? $

Cost Curves - Example:

Cost Curves - do-at-home examples:

• $ c(q) = 10 - 0.5(q-2)^2 + (q-2)^3 $

• Try with all kinds of functions...

Cost minimization in two plants

• Possibly two technologies, therefore two cost functions $ c_1(q_1) \text{ and } c_2(q_2) $

• Graphical approach

  • Use a production-requirement "box"

• Mathematical approach

  • $ \text{minimize} (C = c_1(q_1) + c_2(q_2)) $ subject to: $ q_1 + q_2 = q $

  • replace $ q_2 $ by $ q-q_1 $ and solve $ dC/dq_1 = 0$

  • Solution: $ q_1 \text{ and } q_2 $ such that $ MC_1(q_1) = MC_2(q_2) $

Long-run and short-run cost function - Example.

• $ q = 50 L^{0.5} K^{0.5} $

• Find long run cost function:

  • Total Cost (TC): $ c(w,r,q) = (q/25)(wr)^{0.5} $

  • $ AC(w,r,q) = (1/25)(wr)^{0.5} $

  • $ MC(w,r,q) = (1/25)(wr)^{0.5} $

Long-run and short-run cost function - Example.

• $ q = 50 L^{0.5} K^{0.5} $

• Find short-run cost function ($ K = \bar{K} $):

  • $ L^{SR} = \frac{ q^2 }{ 50^2 \bar{K} } $

  • $ c^{SR}(w,r,q) = w \frac{ q^2 }{ 50^2 \bar{K} } + r \bar{K} $

  • $ {AC}^{SR}(w,r,q) = w \frac{ q }{ 50^2 \bar{K} } + r \frac { \bar{K} }{ q } $

  • $ {MC}^{SR}(w,r,q) = 2 w \frac{ q }{ 50^2 \bar{K} } $

If for example w = 25 and r = 100:

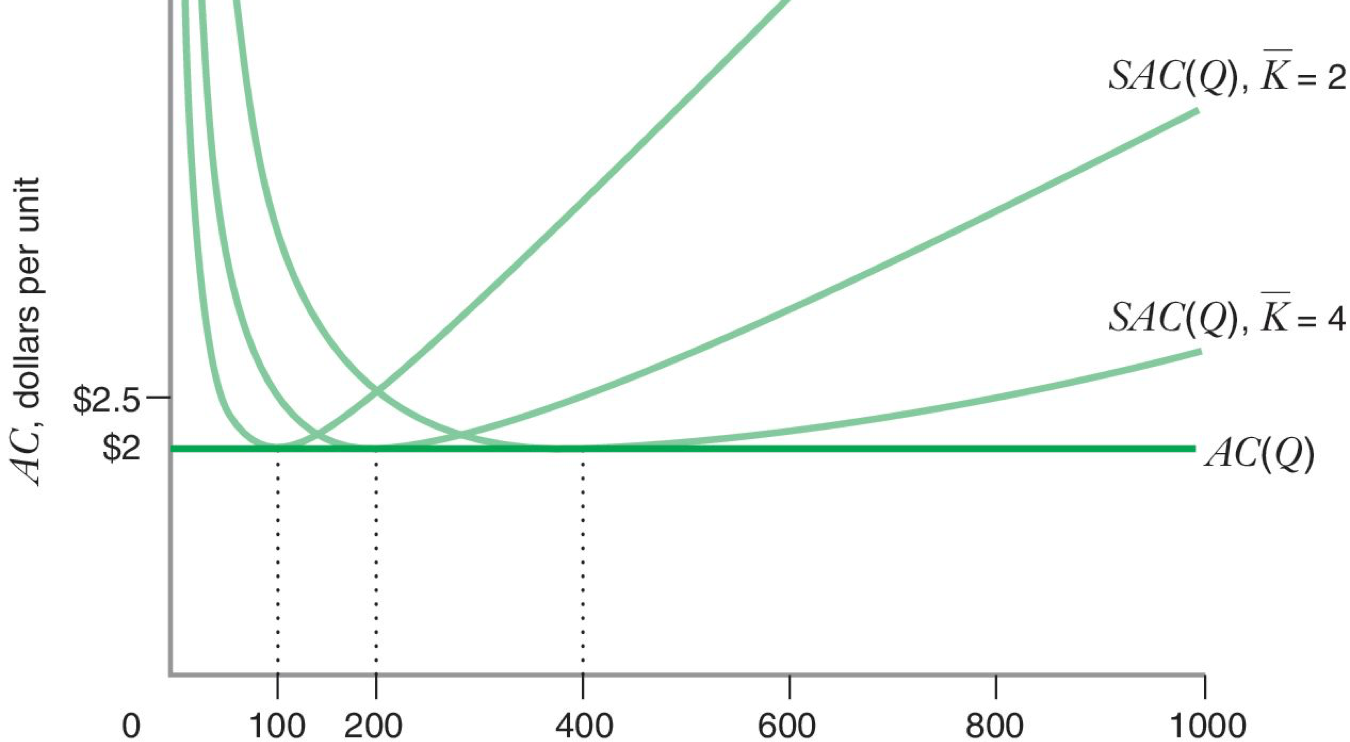
Short-run AC (SAC) and long-run AC (SAC)

• Cost curves coincide if fixed level of capital is also LR solution.

Short-run AC (SAC) and long-run AC (SAC)

• More generally: LR cost curves envelope from below the SR ones.

EconGraphs - general Cobb-Douglas